- Call: +612 8005 0922
- Email: learn@gold-standard.com
- Mon-Fri: 9 AM - 5 PM
While the GAMSAT Maths section does not exist in the real exam, Section 3 does have many problems (in GAMSAT Physics, General Chemistry and Biology) that require basic mathematical skills or manipulations. Keep in mind that ACER banned calculators more than 10 years ago. Many students were surprised by the number of calculations they were required to perform on the real exam. So, is it possible to pass these GAMSAT Maths questions without the help of a calculator?
Well, if you are patient, you will learn that being efficient and using pattern recognition can be very powerful. You CAN actually make "magic" with numbers on the GAMSAT. Below are a few quick and useful tips and formulas to add to your GAMSAT Maths techniques.
* For advice on essential items to bring during the exam, please check out our forum on GAMSAT Test Day Items.
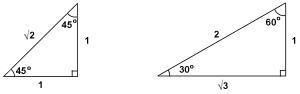
Have you seen these numbers on GAMSAT Physics or GAMSAT Chemistry exams: 1.44, 1.69? Do they ring a bell? You should have memorised all squares between 1 and 15. You likely have 1 to 10 stone cold! 11 squared is 121, 12 is 144, 13 is 169, 14 is 196, 15 is 225 . . . Test makers choose their numbers carefully. The moment you see 1.44 on the GAMSAT, there would be a high likelihood that taking the square root, which gives 1.2, would be required. Pattern recognition, yes?
Sometimes the GAMSAT will say, if B increases by 44%, by what % will A increase? Easy as pie! If B increases by 44%, that is the same as saying 1.44(B) and we know that root 1.44 is 1.2, which means the original sq root B = A has increased by 20%. (Of course, it's not a math test so they won't use "A" and "B" but rather they may present a physics equation to you). Even if they tell you, "given g = 9.8 m/s2," you use 10 unless the answers are very close to each other.
Pi is 3.14, root 2 is 1.4, root 3 is 1.7. Don't be surprised if you need to calculate the perimeter (2 pi r) or area (pi r squared) of a circle. Be comfortable estimating the root of anything! Root 17? Well, the answer must be between 4 and 5 but closer to 4! Check the answers and don't calculate anything if there is only one answer that is between 4 and 4.5.
Fractions will usually permit you to be more efficient. For huge and tiny numbers, you need to be comfy with scientific notation. And if you can hang on to variables for as long as possible, that's even better. You may be surprised how many times mass m ends up being irrelevant as it happily cancels out!
Most past "gamsatters" felt that they rarely used their calculators for GAMSAT Maths. So relax! Be sure that you know the basics and work through all of ACER's practice materials without the use of a calculator and then math will not hold you back!
| sin θ = opp/hyp | cos θ = adj/hyp | tan θ = opp/adj |
| θ = sin-1 x | Estimate square root 3 as 1.7 and root 2 as 1.4 | r2 = x2 + y2 |
A.1 Basic Graphs
A.1.1 The Graph of a Linear Equation
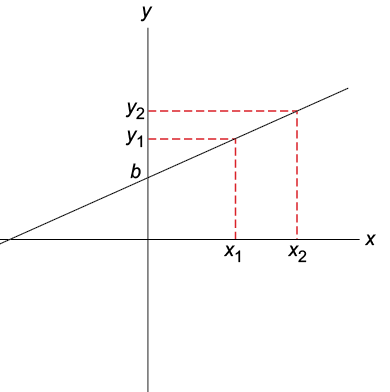
Equations of the type y = ax + b are known as linear equations since the graph of y ( = the ordinate) versus x ( = the abscissa) is a straight line. The value of y where the line intersects the y axis is called the intercept b. The constant a is the slope of the line. Given any two points (x1, y1) and (x2, y2) on the line, we have:
y1 = ax1 + b
and
y2 = ax2 + b.
Subtracting the upper equation from the lower one and dividing through by x2 - x1 gives the value of the slope, a = (y2 - y1)/(x2 - x1).
Note: a positive slope rises as it extends to the right (as in the graph below), a negative descends, and if the line is horizontal, then the slope is zero.
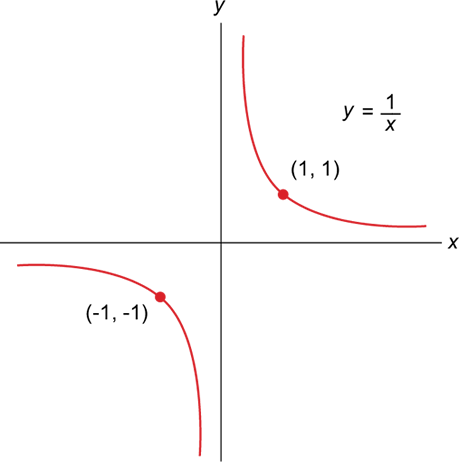
A.1.2 Reciprocal Curve
For any real number x, there exists a unique real number called the multiplicative inverse or reciprocal of x denoted 1/x or x-1 such that x (1/x) = 1. The graph of the reciprocal 1/x for any x is:
A.1.3 Miscellaneous Graphs
There are classical curves which are represented or approximated iin the Gold Standard GAMSAT textbook as follows (if you do not have the book, we suggest doing a Google image search so you can identify these shapes of these graphs/curves): Sigmoidal curve (CHM 6.9.1, BIO 7.5.1), sinusoidal curve (PHY 7.1.1, 7.1.2), and hyperbolic curves (CHM 9.7 Fig III.A.9.3, BIO 1.1.2).
If you were to plot a set of experimental data, often one can draw a line (A.1.1) or curve (A.1.2/3, A.2.2) which can "best fit" the data. The preceding defines a regression line or curve. The main purpose of the regression graph is to predict what would likely occur outside of the experimental data.
A.2 Exponents and Logarithms
A.2.1 Rules of Exponents
A.2.2 Exponential and Logarithmic Curves
The exponential and logarithmic functions are inverse functions. That is, their graphs can be reflected about the y = x line.
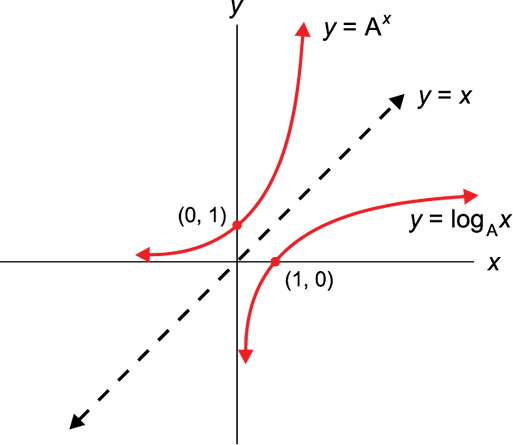
Figure A.1: Exponential and Logarithmic Graphs. A > 0, A ≠ 1.
A.2.3 Log Rules and Logarithmic Scales
The rules of logarithms were discussed in detail in GAMSAT Maths (GM 3.7, 3.8) and in context of Acids and Bases in General Chemistry (CHM 6.5.1). These rules also apply to the "natural logarithm" which is the logarithm to the base e, where "e" is an irrational constant approximately equal to 2.7182818. The natural logarithm is usually written as ln x or loge x . In general, the power of logarithms is to reduce wide-ranging numbers to quantities with a far smaller range.
For example, the graphs commonly seen in the Gold Standard GAMSAT textbooks, including the preceding one, are drawn to a unit or arithmetic scale. In other words, each unit on the x and y axes represents exactly one unit. This scale can be adjusted to accommodate rapidly changing curves. For example, in a unit scale the numbers 1 (= 100), 10 (= 101), 100 (= 102), and 1000 (= 103), are all far apart with varying intervals. Using a logarithmic scale, the sparse values suddenly become separated by one unit: Log 100 = 0, log 101 = 1, log 102 = 2, log 103 = 3, and so on.
In practice, logarithmic scales are often used to convert a rapidly changing curve (e.g. an exponential curve) to a straight line. It is called a semi-log scale when either the x-axis or the y-axis is logarithmic. It is called a log-log scale when both x-axis and y-axis are logarithmic.
Many GAMSAT problems every year rely on a basic understanding of logarithms for pH problems, rate law (CHM 9.10) or a 'random' Nernst equation question (BIO Chapter 0, GS-1). Here are the rules you must know:
For example, let us calculate the pH of 0.001 M HCl. Since HCl is a strong acid, it will completely dissociate into H+ and Cl-, thus :
A.3 Simplifying Algebraic Expressions
Algebraic expressions can be factored or simplified using standard formulae:
A.4 Properties of Negative and Positive Integers
Positive + Positive = Positive
5 + 4 = 9
Negative + Negative = Negative
(-6) + (-2) = -8
Positive + Negative = Sign of the highest number and then subtract
(-5) + 4 = -1
(-8) + 10 = 2
Negative - Positive = Negative
(-7) - 10 = -17
Positive - Negative = Positive + Positive
= Positive
6 - (-4) = 6 + 4 = 10
Negative - Negative = Negative + Positive
= Sign of the highest number and then subtract
(-8) - (-7) = (-8) + 7 = -1
Negative x Negative = Positive
(-2) x (-5) = 10
Positive/Positive = Positive
8/2 = 4
Negative x Positive = Negative
(-9) x 3 = -27
Positive/Negative = Negative
64/(-8) = -8
Here are some challenging math problems, but if you can apply the basic rules then real GAMSAT math (i.e. related to physics and general chemistry problems) will not give you difficulties. The questions are followed by answers and worked solutions/explanations.
1) Simplify the expression: (x2)(y2)(x3)(y)(x0).
x6y3
x5y3
x5y2
xy3
0
2) Simplify the expression: (2x)-2(((2x2)3)2).
16x5
16x6
16x8
16x10
16x12
3) Expand the expression: (x - y + 3)2.
x2 - y2 + 9
x2 + y2 + 9
x2 + y2 + 2xy + 6x + 6y + 9
x2 + y2 - 2xy + 6x - 6y + 9
x2 - y2 - 2xy + 6x - 6y + 9
4) Simplify the expression: (x2a + b)(xa - 2b) / (x2a - b).
xa
xab
xa + 2b
x5a - 2b
x5a + 2b
5) Let x = 4 and y = 8. Evaluate the expression: ((y-2/3)1/2) / (x-1/2).
8
4
1
1/2
1/4
6) Evaluate the expression: log6(24) + log6(9).
3
2
1
1/2
1/3
7) Solve for x: log10(70) = x + log10(7).
0
1
2
3
4
8) Simplify the expression: x(logb(y)) + y(logb(y)).
logb(yx-y)
logb(yx+y)
logb(yxy)
logb(xyxy)
logb(xy)
9) Evaluate the expression: ln (e3)log3(27) + ln (1)ln (e).
e
3
6
3e
9
10) Solve for b: logb(9) - 2(logb(12)) = 2.
¼
½
1
2
4
11) Which equation matches the graph below?
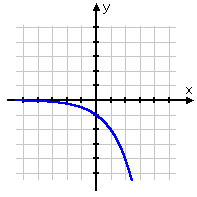
y = 2x - 1
y = -(2x)+ 1
y = 2x
y = -(2x)
y = -(x2)
12) Which equation matches the graph below?
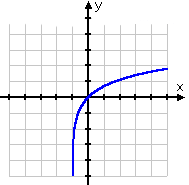
y = ln (x)
y = -ln (x - 1)
y = -ln (x + 1)
y = ln (x - 1)
y = ln (x + 1)
13) As x increases, the slope of f(x) = 2x-1:
14) pH is measured on a logarithmic scale given by the equation pH = - log10(H), where 0 < H <1. As H decreases, the slope of the graph of pH vs H:
1) First rearrange the expression and group like terms:
(x2)(y2)(x3)(y)(x0) = (x2 x3 x0)(y2y)
When multiplying powers with the same base, you can combine them by adding the exponents. For example:
y2y = (y)(y)(y) = y2+1 = y3
So the expression becomes:
(x2 x3 x0)(y2y)
= x2+3+0y2+1
= x5y3
2) We can break this problem two chunks: (2x)-2 and (((2x2)3)2). First consider (2x)-2. Because the exponent is negative, this is equal to the inverse of the positive power.
(2x)-2 = 1/(2x)2
Next, distribute the exponent throughout the parenthetical expression:
1/(2x)2 = 1/(22x2)
Now lets move to our second chunk, (((2x2)3)2). When you raise a power to another power, multiply the exponents together. And don't forget to distribute through the parenthetical expression.
(((2x2)3)2) = ((23x(2)(3))2) = (2(3)(2)x(2)(3)(2)) = 26x12
Finally, let's multiply the two chunks together to get back to the original expression:
(2x)-2(((2x2)3)2)
= [1/(22x2)](26x12)
= (26x12)/(22x2)
When dividing powers, subtract the exponents:
= (26-2x12-2)
= 24x10
= 16x10.
3) When raising a polynomial to a power, treat everything inside the parentheses as if it was a single value. So (x - y + 3)2 is really (x - y + 3)(x - y + 3), NOT (x2 - y2 + 32). Now let's multiply and expand:
(x - y + 3)(x - y + 3)
= x2 - xy + 3x - xy + y2 -3y + 3x - 3y + 9
= x2 + y2 - 2xy + 6x - 6y + 9
4) First simplify the numerator:
(x2a + b)(xa - 2b) / (x2a - b)
= (x2a+b+a-2b) / (x2a - b)
= (x3a - b) / (x2a - b)
Then combine the numerator and denominator using the properties of exponent division.
= (x3a-b-2a+b)
= xa
5) First combine the exponents where possible, and rearrange so they are all positive:
((y-2/3)1/2) / (x-1/2)
= (y-1/3) / (x-1/2)
= (x1/2) / (y1/3)
Now plug in x = 4 and y = 8. Notice that 4 = 22 and 8 = 23.
= (41/2) / (81/3)
= (2(2)1/2) / (2(3)1/3)
= 21/21
= 1.
6) When adding logarithms of the same base, combine them by multiplying the numbers in parentheses. In this case:
log6(24) + log6(9)
= log6(24*9)
= log6(216)
= log6(63)
Now remember, a logarithm is an exponent. The question it poses is, "the base raised to what power is equal to the number in the parentheses?" So 6 raised to what power is equal to 63? The answer is, of course, 3.
7) First isolate the x terms on one side and all other terms on the other side of the equation.
log10(70) = x + log10(7)
log10(70) - log10(7) = x
Now combine the logarithms. When subtracting logarithms of the same base, combine them by dividing the numbers in parentheses.
log10(70/7) = x
log10(10) = x
1 = x.
8) A coefficient multiplied by a logarithm can by brought inside the parentheses as an exponent.
x(logb(y)) + y(logb(y))
= logb(yx) + logb(yy)
= logb(yxyy)
= logb(yx+y).
9) The natural log has base e. Note that a logarithm of 1, no matter what the base, is equal to 0. And a log of its own base is equal to 1. So:
ln (e3)log3(27) + ln (1)ln (e)
= ln (e3)log3(27) + 0*1
= 3 log3(27)
= 3(3)
= 9.
10) First simplify the logarithms on the left side.
logb(9) - 2(logb(12)) = 2
logb(9) - logb(122) = 2
logb(9/144) = 2
logb(1/16) = 2
Now convert the equation into exponent form using the definition of logarithms.
b2 = 1/16
b = √(1/16)
b = ¼.
11) There are some useful pieces of information to notice that will help you answer this type of problem.
- What is the x and/or y intercept, if there is one?
- Where is the vertical asymptote? [Note: an 'asymptote' refers to a line that keeps approaching a given curve but does not meet the curve at any finite distance.] And does the curve approach positive or negative infinity?
In this case there is no x intercept, but the y intercept is at the point (0, -1). Plugging x = 0 into the given equations we can rule out all options except y = -(2x), so that is the solution.
12) There are some useful pieces of information to notice that will help you answer this type of problem.
- What is the x and/or y intercept, if there is one?
- Where is the vertical asymptote? And does the curve approach positive or negative infinity?
The x and y intercept of this graph are the same, at (0, 0). Plugging in y = 0 to the given equations we can eliminate all but y = ln (x+1) and y = -ln (x+1). Next find the vertical asymptote. It appears to be located at x = -1, and the curve approaches negative infinity. When x is small, -ln (x+1) is positive, so it cannot be the solution. Thus the graph represents y = ln (x+1).
13) The -1 in the exponent of f(x) = 2x-1 does not change the behavior of the slope, it simply shifts the graph along the x-axis. The slope of f(x) = 2x increases exponentially as x increases.
14) You can think of pH and H as corresponding to y and x respectively. So the graph you are considering is y = -log10(x), the logarithm graph reflected about the x-axis. So the slopes along the curve are the opposite of the positive logarithm graph. Therefore when we decrease the value of x (moving right to left along the axis) the slope increases. If you are unsure of your solution, plug in test points to check.
Discuss any of our GAMSAT maths questions or worked solutions here: GAMSAT Math Forum
If you come from a non-science background, you can find our preparation advice here: Non-Science Background: GAMSAT Preparation
Get 1 full hour access to free GAMSAT Physics and GAMSAT Chemistry and Biology videos online. Register here: Free GAMSAT-prep User Account
To help you prepare for the exam, Gold Standard GAMSAT has assembled comprehensive information on GAMSAT scores, topics covered, preparation advice, free GAMSAT sample questions and other study resources.